Abstract:
The aim of this activity is to make students aware of the scales and spatial hierarchies in nature and of the magnitudes represented by the different units of measurement. It is also intended that they practice and gain agility in the calculation of proportions in the representation of large magnitudes on a human scale. As a practical example, the representation of the Solar System is used, scaling the real distances between the Sun and the planets to classroom, playground and even neighborhood proportions.
| Learning objectives: To be aware of the magnitudes in real life represented by units of measurement To understand proportions and scales in maps, object models and scientific models. To understand the meaning of operating with powers in mathematics.To apply critical thinking in front of media, images, and illustrations. |
To practice teamwork, organisation, and communication skills
| Teachers’ profile: (team transversality) Mathematics, Natural Sciences. |
Advisable age of students: 13-14 Attention to diversity and inclusion aspects to have in account
Previous knowledge: Mathematics of division, proportions, and ratios.
Total duration: 3 hours
Materials:
Digital and interactive resources indicated below,
- Rules, measuring tape, callipers, strings, and objects in the classroom to measure
- Black or white board, or projector
- Pencils, erasers and papers or notebooks,
Balls (porex, foam, papermache,…) of different sizes to represent Sun and planets, or cards with printed images of planets, or costumes representing planets.
- String
Phase 1 30 min Visualisation
Development
The class or project will start with the visualisation of the 1977 video “Powers of Ten” (it has subtitle translation to many languages andalso other language versions exist).
After that, in teams of 2-3 people, students will explore the application “Scale of the Universe” starting at human scales and exploring deeply in the immediate lower and higher range, and then
Phase 2 2 hours Artistic action and experimentation
Development:
- Review of space units and what they mean in daily life: The phase starts with a reminder, sharing and collecting previous knowledge of spatial units and the magnitude of things they represent. With callipers, rulers, measuring tape and strings students can measure materials and objects in class, from grain size objects, through middle size objects (tables, chairs), to the distancesbetween walls. While doing so, they will encounter magnitudes of mm, cm, and meters. Reflection about distances to the playground or to the next village can be also done (100s of meters, km). In this process the mathematical concepts of powers of ten when they jump from magnitude to magnitude (ex: cm to m) can be done.
- Elaboration of classroom architectonic plan at scale: In an organized teamwork the students measure the dimensions of the classroom floor and shapes (narrower areas, doors, etc). A sketch of it is drawn on the board (not to scale but with the measured dimensions annotated). Students, in teams of two draw in their notebooks a scaled version of the classroom floor plan (1:100 or 1:200 depending on paper size). The aim is to understand proportions and scaling of models. At the teacher’s choice a different object per team can be proposed to be drawn at scale (table, bike, etc..)
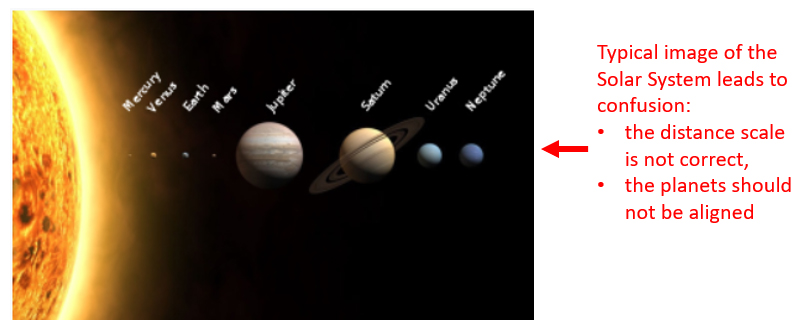
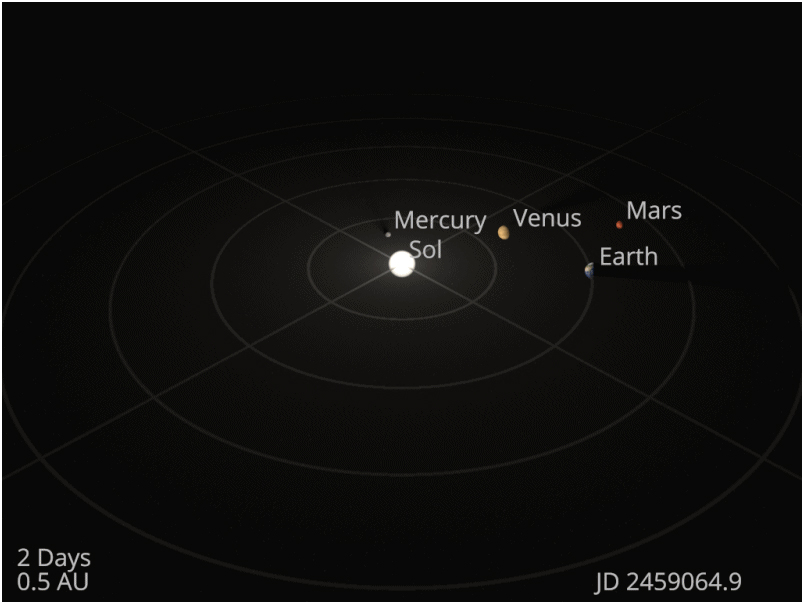
Representation of the distances between Solar System’s planets and the Sun at scale. A table with the numeric distance of every planet to the Sun will be posted in the screen or board. It will be explained that we are going to scale 4 million of kilometres to 1 cm. Then the equivalent distances will be written beside de real ones in the board (it will go from 14 cm for Mercury, to 11 m for Neptune). The inner planets will be quite close between them, while for the outer planets there will be gaps of several meters (see table below). In teams of 10 students, they are going to represent the Solar System scaling the distances (but not the size of the planets and sun at the same time because we would need km): in each team 9 students there will be the Sun and every one of the planets, the 10th student will be a conductor to help with the material and observing how everybody is in place. The students can hold a card with the picture of the stellar object they represent, or they can wear a costume representing it, or they can hold a porex ball painted as their planet. It must be clear that they have not to be aligned pointing in line to the Sun: each planet it’s at a different place of its orbit (at the right distance) and there’s no alignment (see figures below).
Phase 3: 30 min Reflexion and debate
Development:
The students sit down again in rounds and talk about the experience and what they understand about it, reviewing the concepts.
They can also debate about critical thinking in reference to the interpretation of images, like the illustrations of the Solar System where planets appear aligned (when they shouldn’t be) or all looking equally separated.
This activity can be used as an opportunity to organize a focus group on the learning methodology, focusing the discussion on whether students think they have learned better or worse the concepts covered in this activity compared to other more traditional ones.
Comments, possible derivations, and prolongations of the proposal:
This proposal can have many derivations and can be part of a long project. The mathematics needed for it (for example to scale the distances in the Solar System) can be not only posted in the board but calculated by the students. The teacher can also propose the following challenge:
- Not only distances could have been taken in account. If we had considered the size of the objects of the Solar System (Sun and Planets), as well as the distances, would we had been able to represent it in the classroom or the playground? (Suppose earth diameter is 1cm, it would be at 125 m from the Sun, and Neptune would be at 4 km). This video is illustrative of this fact:
On a dry lake in Nevada, a group of friends build the first scale model of the Solar System with complete planetary orbits: a true illustration of our place in the universe.
References and links:
- Scales of the Universe: zoom application https://htwins.net/scale2/
- Circular representation of the observable Universe on logarithmic scale

Created especially for Wikipedia.org by Pablo Carlos Budassi
This file is licensed under the Creative CommonsAttribution-Share Alike 3.0 Unported license.
Circular representation of the observable universe on a logarithmic scale. Distance from Earth increases exponentially from center to edge. Celestial bodies were enlarged to appreciate their shapes.
Artist’s logarithmic scale conception of the observable universe with the Solar System at the center, inner and outer planets, Kuiper belt, Oort cloud, Alpha Centauri, Perseus Arm, Milky Way galaxy, Andromeda galaxy, nearby galaxies, Cosmic Web, Cosmic microwave radiation and Big Bang’s invisible plasma on the edge.
4- Things to measure in class (together with chairs, tables, floor, walls…)
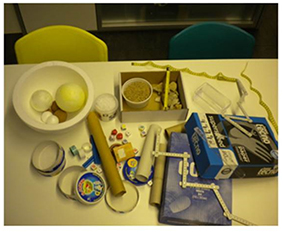
5- Example of material to represent Solar System Planet’s relative distances at classroom scales: The sun and every planet it’s held by a student, stretching the string to the represented distance from the Sun at the right scale. The stellar objects can be represented by children with costumes, balls, etc…