MATHEMATICS
Abstract: On the occasion of the screening of a video about the ancient theater of Epidaurus, reference is made to the concept of the inscribed angle. Students then discover the properties of the inscribed corners in the circles of the football and basketball courts located in the school yard.
Learning objectives:
the concept of an inscribed angle in a circle,
• The relationship between the inscribed and the corresponding central angle,
• The relationship between the inscribed angle and the corresponding arc,
• The relationship of the inscribed angles that go into the same arc
- The measure of the inscribed angle that ends in a semicircle.
Teachers’ profile: Mathematician(team transversality)
MATERIALS
Twine,string, paper tape, tape measure, protractors, rulers, cardboard, markers.
Advisable age of students: (Flexible according to the curriculum of specific country) 14 years old |
Previous knowledge:
Circle, radius, diameter, concentric angle, corresponding arc
Total duration: 2 teaching hours
PHASE A Visualisation Duration: 15 min
The lesson started with two short videos about the ancient theatre of Epidaurus. The first video lasting 2.31min entitled “The ancient theatre of Epidaurus, the archaeological site and the museum” and the second lasting 0.56 min entitled “The ancient Greek theatre, the parts of the theatre”.
A discussion followed about the shape of the theatre and why the ancients built their theatres in a circular shape. The majority of responses were related to acoustics, while few were related to visibility. The teacher mentioned that the spectators sitting in the same row saw the scene from the same angle. When asked by the students how this is done, the teacher said that the answers will be given in the courtyard. Meanwhile, a rough shape was given on the board and the students learned what an inscribed angle means
PHASE B Artistic action and experimentation Duration: 30 min
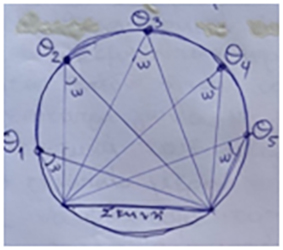
The students, accompanied by the teacher, were taken to the school yard. Half of the students took with them a chair, while the rest took protractors, rulers, cardboard, string and markers. They were driven into the center of football’s great circle. The students with the chairs were placed around the circle like the spectators in the stands. With the paper tape the students created a circle chord (stage) and the actors were placed on it. They created inscribed corners with viewer vertices and edges, the ends of the paper tape. Then another group of students placed cardboard under the string at the vertices of the inscribed angles, measured and recorded the measures of the inscribed angles. They noticed that they all found the same result.
Next stage was the measurement of the focal angle which had the same edges (of the scene) as the inscribed angles. They found it to be twice as much. The last part of this activity was to find the measure of the inscribed angle that ended up in this large semicircle (always with the string and paper tapes to stick it to the ground). They found that they were dealing with a right angle.
.PHASE C Reflexion and debate Duration: 45 min
The next lesson held in the classroom (they liked it much more in the courtyard) we tried to classify the conclusions we found:
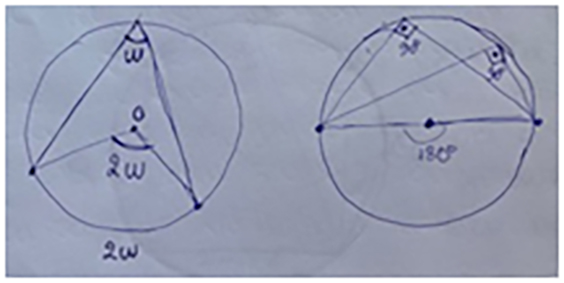
- Inscribed angles ending in the same arc are equal to each other.
- The measure of the inscribed angle is half the measure of the epicenters that terminate on the same arc.
- Inscribed angles ending in a semicircle are right.
- The measure of the inscribed is half the measure of its corresponding arc.
We dedicated the rest of the teaching hour to solving applications on the board, to all the above that the students learned experientially.
References and links: