| Abstract: |
Learning objectives:
|
| Advisable age of students: (Flexible according to the curriculum of specific country) 14 years old |
Previous knowledge: Comparable sums
Materials: Bicycle, Gymnastic Hoop, Round Table, CD, Coins, Paper Tape, Tape Measure
Total duration: 2 teaching hours
PHASE A Visualisation (15 min)
In class we saw a video from YOUTUBE or by ERT (national Greek Television) with the title: “The Olympic circles in the sky of the stadium. TOKYO: Closing ceremony” at the 32nd Olympic games where they formed Olympic circles in the sky of the stadium. This was followed by a discussion about the Olympic games and the Olympic cycles. Then the teacher drew a circle on the board and explanations were given with basic concepts “radius, diameter, arc, chord”.
PHASE B Artistic action and experimentation (30 min)
Development: the students, accompanied by the teacher, were taken to the school yard. While moving around the school grounds, they spotted objects in a circular shape (circular discs in the classroom, a gymnastic hoop, and a bicycle in the courtyard, a round table in the corridor). Divided into groups, the students carefully wrapped the circular objects with paper tape, and measured the diameter of the objects with a tape measure. Next, the groups of students peeled off the paper tapes and placed them stretched on the chair and on the classroom floor.
Then, with tape measures, they measured the lengths of the paper strips and they recorded them in a table below their respective diameters
Diameter (δ) | ||||
Cycle Length (L) |
PHASE C Reflexion and debate (45min)
In the next lesson we “learned division”.
The students – working in groups – divided the length of the corresponding circular object by its diameter and the “miracle” happened: the results were almost the same (about 3 something – 3.14)
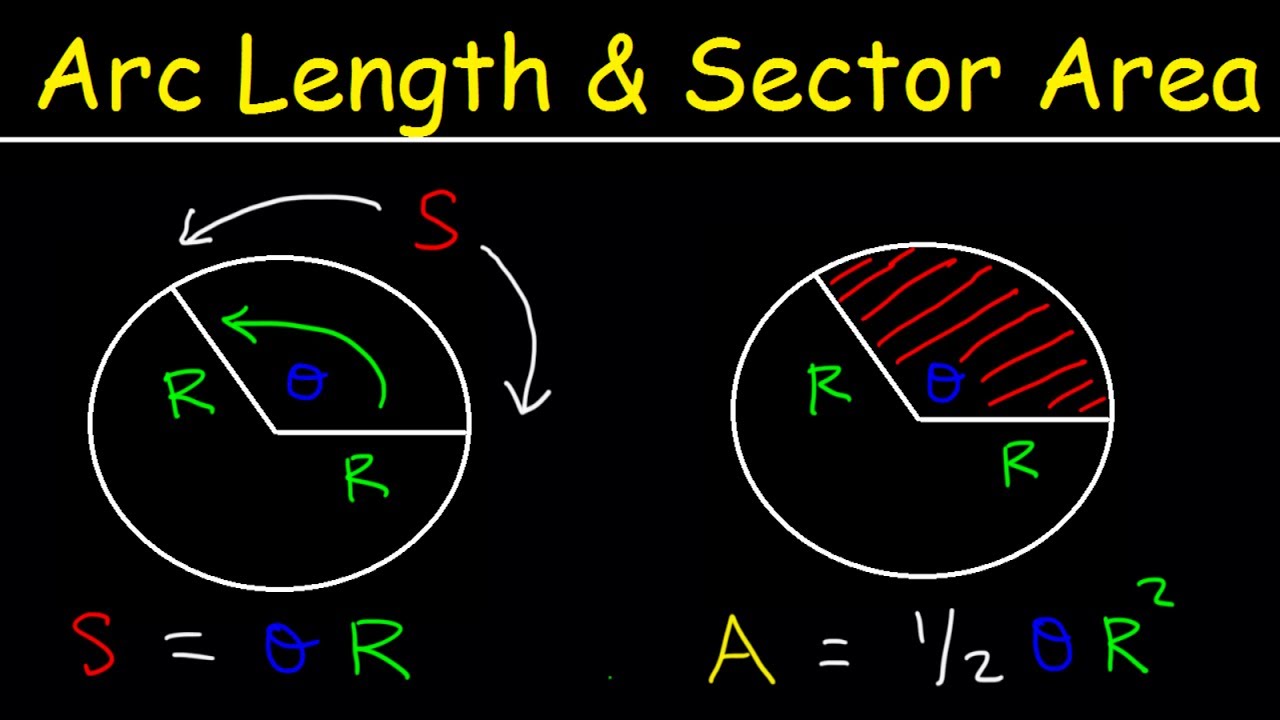
We discussed this by saying that the amounts are proportional and that this quotient is symbolized all over the world with the small Greek letter “π” initial letter of the word “periphery”. We also mentioned the importance of the constant “π” and how much the ancient mathematicians had approached it, but also how today’s mathematicians deal with the constant “π”. Next, we read some texts about the constant “π” and wrote some decimals for it. As the next stage, we were concerned with the relationship that connects the length of the circle with its diameter (L=π*δ). Applications and problems that verified our results followed.
References and links:
https://www.youtube.com/watch?v=5c3vbDuG3RI